Fenwick Tree
Suppose A is an array of length n. A Fenwick tree, or a Binary Indexed Tree, is a data structure that can:
- be created in \(O(n)\) time;
- update or retrieve the value of an element of A in \(O(\log n)\) time;
- find a range sum in \(O(\log n)\) time.
Description
A Fenwick tree is implemented as a flat array where each element is equal to the sum of numbers in a certain range. The following image shows a possible interpretation of the Fenwick tree as a tree. The nodes of the tree show the ranges they cover.
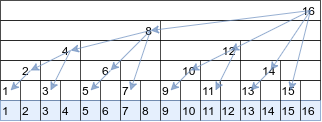
Each element contains the sum of the values since its left sibling (or since zero if there are no left siblings). A prefix sum can be calculated by adding the value of the element and all its left siblings. Incrementing an element requires incrementing all the elements in the upward chain to the root.
Implementation
The left sibling and the parent of a node can be found by simple bitwise operations:
left_sibling(i) = i - i & (-i)
parent(i) = i + i & (-i)Hence the tree can be implemented as a flat array (indexing starts at 1):
class Fen:
def __init__(self, n):
self.fen = [0]*n
self.n = n
def add(self, i, val):
assert i > 0
while i < self.n:
self.fen[i] += val
i += i & -i
def sum(self, i):
ans = 0
while i > 0:
ans += self.fen[i]
i -= i & -i
return ansThese two methods are all we need to solve the problem from the previous posts:
You are given an integer array nums and you have to return a new counts array. The counts array has the property where counts[i] is the number of smaller elements to the right of nums[i].
Here is how we solve it in \(O(n \log n)\) time with a Fenwick tree:
- Sort the numbers and find each number’s rank.
- Go through numbers from right to left, insert each number’s rank into the tree, and compute the sum of all smaller ranks.
def right_and_smaller3(nums):
m = {num:rank+1 for rank, num in enumerate(sorted(set(nums)))}
tree = Fen(len(nums))
result = []
for num in reversed(nums):
rank = m[num]
result.append(tree.sum(rank - 1))
tree.add(rank, 1)
return reversed(result)That’s it! An efficient solution in 25 lines of code.
There are more things that a Fenwick tree can do:
- initialize in \(O(n)\) time
@classmethod
def from_array(self, nums):
#O(n) initialization
n = len(nums) + 1
tree = Fen(n)
s = 0
fen = [0]
#store cumulative sums
for num in nums:
s += num
fen.append(s)
for pos in reversed(range(1, n)):
fen[pos] -= fen[pos - (pos & -pos)]
tree.fen = fen
return tree- update an element in \(O(\log n)\) time.
Updating an element can be done by adding new value minus current value.
def update(self, i, val):
self.add(i, val - self.get(i))- retrieve an element in \(O(\log n)\) time.
To get the value of an element, we subtract all of its children. Alternatively, we could just store the original array, taking up additional \(O(n)\) memory, but retrieving elements in \(O(1)\) time.
def get(self, pos):
ans = self.fen[pos]
c = 1
i = pos
while i % 2 == 0:
ans -= self.fen[pos - c]
i = i >> 1
c = c << 1
return ansIn the next post, I’ll introduce the heap data structure.